Karan Shah
"Chaos: When the present determines the future, but the approximate present does not approximately determine the future." - Edward Lorrez
Abstract¶
Chaotic processes are systems that are highly sensitive to initial conditions. A famous example of a chaotic process in the butterfly effect: a tornado in Georgia is the result of a butterfly flapping its wings in China. The only way to predict chaotic system is analytically. For systems of many variables, eg weather, chemical reactions etc, running an analytically calculating the state of the system at each time step would require a prohibitive amount of computation. In this project, I use a technique called Reservoir Computing with a reservoir being a class of Recurrent Neural Networks called Echo State Networks to predict the two chaotic systems: Mackey-Glass, consiting of only one time-varying variable and Chua's Circuit, consisting of three time varying variables. While my learner is effective at learning Mackey-Glass, predicting Chua's circuit works well only for short amounts of time.
Introduction¶
A chaotic system is one in which infinitesimal differences in the starting conditions lead to drastically different results as the system evolves. This makes it impossible to predict the state of the system at a time point in the non-immediate future.
A double pendulum is an example of a chaotic system, consisting of a pendulum attached to the bob of another pendulum. It is characterized by two parameters: $ \theta_1$ and $ \theta_2$, which are the initial positions of the two bobs. The following simulation[1] shows how a small variation in the initial position leads to a wide difference in the motion of the pendulums:
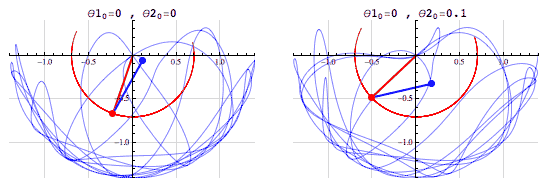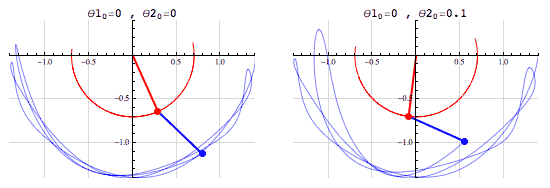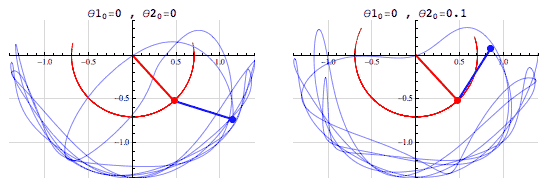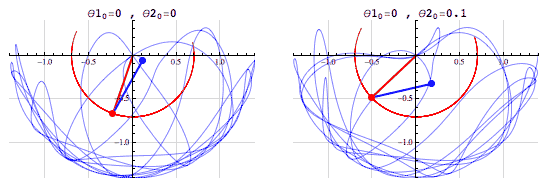

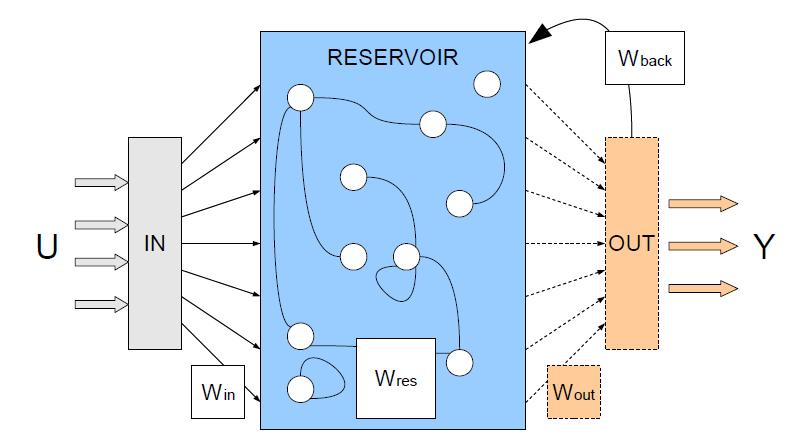
Reservoir Computing (RC) is a machine learning algorithm using a reservoir and an output learner. The reservoid itself is a random but fixed recurrent neural network(RNN). Here, random but fixed means that the edges and weight of the RNN are initialized randomly and kept fixed for training and testing. The output learner is a linear transformation of the reservoir output. Any learning algorithm can be used as an output learner, from simple linear rigression to convolutional neural networks. The following diagram shows the general structure of an RC learner, where $U$ is the input and $Y$ is the prediction:

Title¶
Tiamath is the Babylonian Goddess of Chaos and Water. Seemed apt for a project studying chaos using reservoir computing.
Background¶
Chaotic Systems¶
A chaotic system is characterized by [2]:
Having a dense collection of points with periodic orbits,
Being sensitive to the initial condition of the system (so that initially nearby points can evolve quickly into very different states), a property sometimes known as the butterfly effect, and
Being topologically transitive.
In this project we will study chaotic systems consisting of coupled differential equations. A coupled system is of the form: $$ \frac{dx}{dt} = f(y) $$ $$ \frac{dy}{dt} = f(x) $$
where $x \& y$ are time-dependent, that also fulfils the criteria listed above.
Reservoir Computing¶
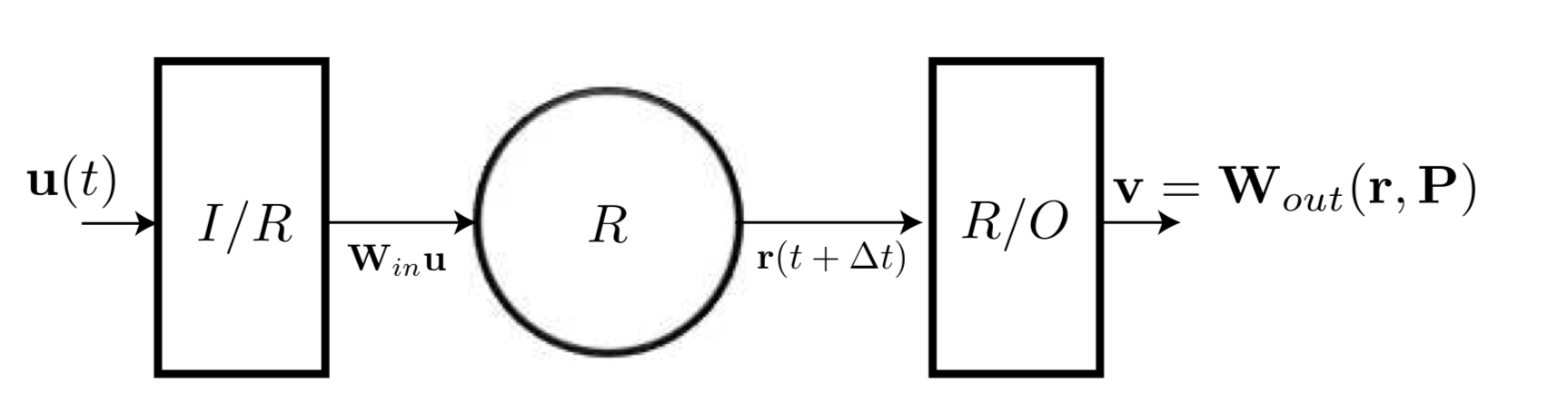
For this project, we focus on time series data $\textbf{u}$, where vector $\textbf{u}(t)$ is the state of the system at time $t$. The learner consists of an input layer $\textbf{W}_{in}$ a reservoir $R$ and an output layer $\textbf{W}_{out}$. The reservoir $R$ is initialized as a graph of $D_r$ nodes with random weights and an activation function $tanh$. The input to the reservoir is $\textbf{W}_{in}\textbf{u}(t)$ and the output is $\textbf{W}_{out}(\textbf{r},P)$ where $\textbf{r}$ is the state of the reservoir and $P$ are parameters to of the output learner.
The following figure shows an example reservoir:


Training¶
The state of the reservoir at time $t+1$ is given by
$$ \textbf{r}(t+1) = tanh[\textbf{Ar}(t) + \textbf{W}_{in}\textbf{u}(t)] $$
where $\textbf{A} $is the Adjacency Matrix of the Reservoir graph.
The output is
$$ \textbf{v}(t+1) = \textbf{W}_{out}(\textbf{r}(t+1), P) $$ and the output learner is trained on correct prediction $\textbf{u}(t+1)$

Prediction¶
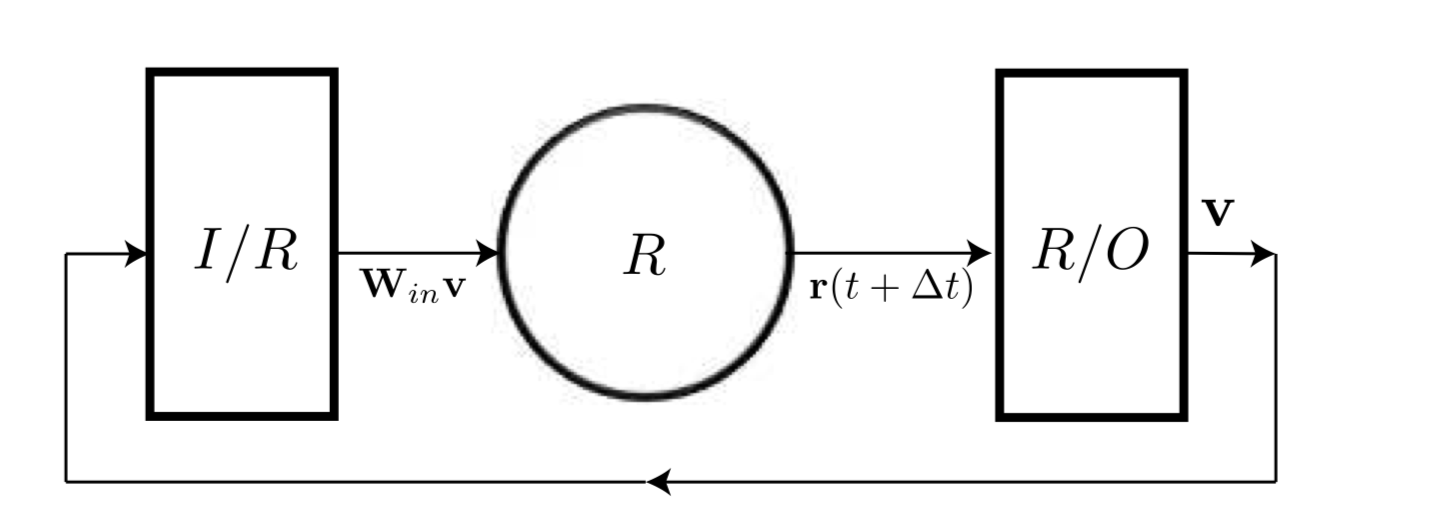
To generate prediction, the output at time $t$ is fed in as the input for time $t+1$.
The state of the system at time $t+1$ is given by:
$$ \textbf{r}(t+1) = tanh[\textbf{Ar}(t) + \textbf{W}_{in}\textbf{W}_{out}(\textbf{r}(t),P)] $$
where $ \textbf{v}(t) = \textbf{W}_{out}(\textbf{r}(t), P) $ is the prediction for $\textbf{u}(t)$

Motivation¶
Chaotic systems are notorisously difficult to predict. But if successfully predicted, they have a wide range of applications, ranging from weather forcasting, chemical simulations, control systems, etc.
Reservoir computing benefits from relatively lower training costs, as compared to traditional RNNs and LSTMs, because of the actual weights of the reservoir RNN are initialized randomly and then kept fixed. Only the output learner is trained. They have been shown to successfully predict chaotic systems for non-intermediate times [3, 4, 5] for simple cases. In this project, I reproduce the often studied Mackey-Glass system and apply RC to Chua's Circuit for the first time.
Experiments and Results¶
The design decisions for my experiments were:
- Reservoir Size $R_n$
- Output learner: Ridge Regression with Regularizer $\lambda$
- Training Time Period
I use the standard MSE as my error metric for the experiments.
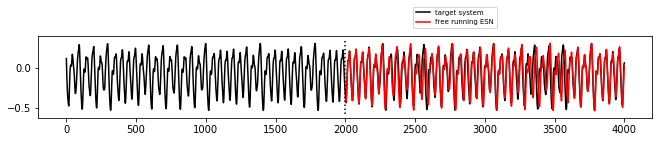
Mackey-Glass¶
The Mackey-Glass equation is the nonlinear time delay differential equation: $$ \frac{dx}{dt} = \beta \frac{x_{t-\tau}}{1+x_{t-\tau}} - \gamma x$$
It shows chaotic dynamics depending on the values of the parameters $\beta, \gamma, \tau$
I generated data for this system using a matlab script with the ode45 solver. The parameters used were: $\beta = 0.2$, $\gamma = 2$, $\tau = 17$.
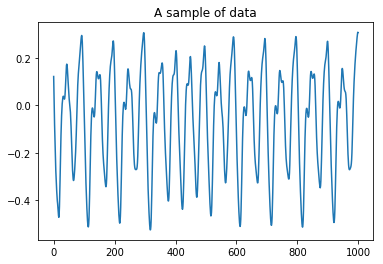
To understand reservoir computing, I wrote a python script following the above equations using Numpy and Scipy.
The hyperparameters for this results are:
- Reservoir Size 1000
- Training 2000 time steps
The error on predicting 2000 timesteps was 2.8025401143798896e-07
Prediction diagram:
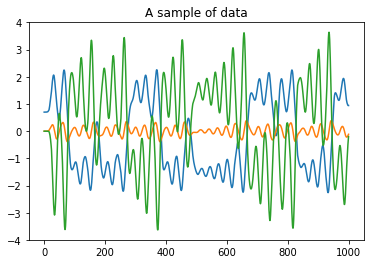
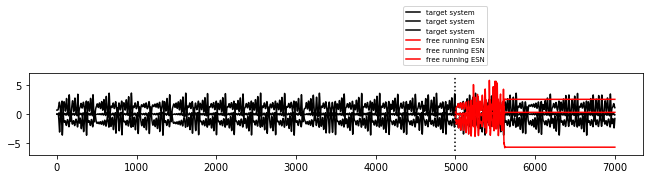
Chua's Circuit¶
Data:
Results: 3.458336973289916 error
TODO¶
- Explain Chua's Circuit
- Discuss/Conclude results
- Clean code and open source it
- References